TRIGONOMETRY LAWS AND IDENTITIES DEFINITIONS sin(x)= Opposite Hypotenuse cos(x)= Adjacent Hypotenuse tan(x)= Opposite Adjacent csc(x)=TRIGONOMETRIC IDENTITIES Reciprocal identities sinu= 1 cscu cosu= 1 secu tanu= 1 cotu cotu= 1 tanu cscu= 1 sinu secu= 1 cosu Pythagorean Identities sin 2ucos u= 1 1tan2 u= sec2 u 1cot2 u= csc2 u Quotient Identities tanu= sinu cosu cotu= cosu sinu CoFunction Identities sin(ˇ 2 u) = cosu cos(ˇ 2 u) = sinu tan(ˇ 2 u) = cotu cot(ˇ 2 u) = tanu csc(ˇ 2 u) = secu sec(ˇ 2 u) = cscuSin 2t = 2 sin t cos t cos 2t = cos 2 t – sin 2 t = 2 cos 2 t – 1 = 1 – 2 sin 2 t Less important identities You should know that there are these identities, but they are not as important as those mentioned above They can all be derived from those above, but sometimes it takes a bit of work to do so The Pythagorean formula for tangents
What Are The Quotient Identities For A Trigonometric Functions Socratic
Tan 2 x trig identity
Tan 2 x trig identity-Following identities 1 secAtan A = 1sin A cosA 2 tan Acot A =secA cosecA 3 sec 2 θcosec2θ=sec2 θcosec2 θ 4 cosecθ−cotθ 1−cosθ =cosecθ 5 cosec x −sinx =cosx cot x 6 1cos 4 x −sin4 x =2cos2 x 7 secθtanθ= cosθ 1−sinθ 8 sin A tan A 1−cosA =1secA Chapter 15 Further Trigonometry 2 152 The addition formulae A proof of the formula for sin (AB) will be givenTrigonometric identities are equalities involving trigonometric functions An example of a trigonometric identity is sin 2 θ cos 2 θ = 1 \sin^2 \theta \cos^2 \theta = 1 sin2 θcos2 θ = 1 In order to prove trigonometric identities, we generally use other known identities such as Pythagorean identities




Tangent Half Angle Formula Wikipedia
We have certain trigonometric identities Like sin 2 θ cos 2 θ = 1 and 1 tan 2 θ = sec 2 θ etc Such identities are identities in the sense that they hold for all value of the angles which satisfy the given condition among them and they are called conditional identities Trigonometric Identities With Examples Example 1 Prove the following trigonometric identities (i) (1 – sin 2Sine, cosine, secant, and cosecant have period 2π while tangent and cotangent have period π Identities expressing trig functions in terms of their supplements Sum, difference, and double angle formulas for tangent The half angle formulas The ones for sine and cosine take the positive or negative square root depending on the quadrant of the angle θ/2 For example, if θ/2 is an Explanation Change to sines and cosines then simplify 1 tan2x = 1 sin2x cos2x = cos2x sin2x cos2x but cos2x sin2x = 1 we have ∴ 1 tan2x = 1 cos2x = sec2x Answer link
Integrals requiring the use of trigonometric identities 2 3 Integrals involving products of sines and cosines 3 4 Integrals which make use of a trigonometric substitution 5 wwwmathcentreacuk 1 c mathcentre 09 1 Introduction By now you should be well aware of the important results that Z coskxdx = 1 k sinkxc Z sinkxdx = − 1 k coskx c However, a little more care is needed when weCos x/2 ≠ ½ cosx;Tan x/2 ≠ ½ tanx Example 2 Find exact value for, tan 30 degrees, without a calculator, and use the half angle identities (refer to the Unit Circle)
Answer to Verify the trigonometric identity cos^2 theta (1 tan^2 theta) = 1 By signing up, you'll get thousands of stepbystep solutions to#sin 2theta = (2tan theta) / (1 tan^2 theta)# #cos 2theta = (1 tan^2 theta) / (1 tan^2 theta)# sankarankalyanam 1 How do you use a double angle identity to find the exact value of each expression?• Note sin x/2 ≠ ½ sinx;



What Are The Quotient Identities For A Trigonometric Functions Socratic
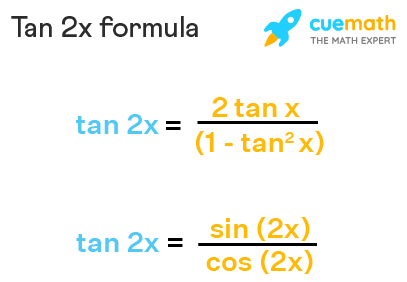



Tan 2x Formula What Is Tan 2x Formula Examples
0以上 tan^2 trig identity Tan^2 trig identity Math Cheat Sheet for Trigonometry This website uses cookies to ensure you get the best experienceYou have seen quite a few trigonometric identities in the past few pages It is convenient to have a summary of them for reference These identities mostly refer to one angle denoted θ, but there are some that involveIdentities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify Statistics Arithmetic Mean Geometric Mean Quadratic Mean Median Mode Order Minimum Maximum Probability MidRange Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal DistributionBy dividing the identity sin2 θcos2 θ ≡ 1 by (a) sin2 θ (b) cos2 θ obtain two further identities Hint Recall the definitions of cosecθ, secθ, cotθ Your solution Answer (a) sin 2θ sin2 θ cos2 θ sin 2θ = 1 sin θ (b) sin θ cos 2θ cos2 θ cos θ = 1 cos2 θ 1 cot2θ ≡ cosec2θ tan2 θ 1 ≡ sec2 θ Key Point 13 introduces two further important identities Key Point



7 Proving Ids Trig Functions Identities




How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic
Free trigonometric identity calculator verify trigonometric identities stepbystep This website uses cookies to ensure you get the best experience ByTan(x y) = (tan x tan y) / (1 tan x tan y) sin(2x) = 2 sin x cos x cos(2x) = cos 2 (x) sin 2 (x) = 2 cos 2 (x) 1 = 1 2 sin 2 (x) tan(2x) = 2 tan(x) / (1 Using basic trig identities, we know tan(θ) can be converted to sin(θ)/ cos(θ), which makes everything sines and cosines $$1 − cos(2θ) = ({sin(θ)}/{cos(θ)}) sin(2θ)$$ Distribute the right side of the equation $$1 − cos(2θ) = 2sin^2(θ)$$ There are no more obvious steps we can take to transform the right side of the equation, so let's move to the left side We can use the
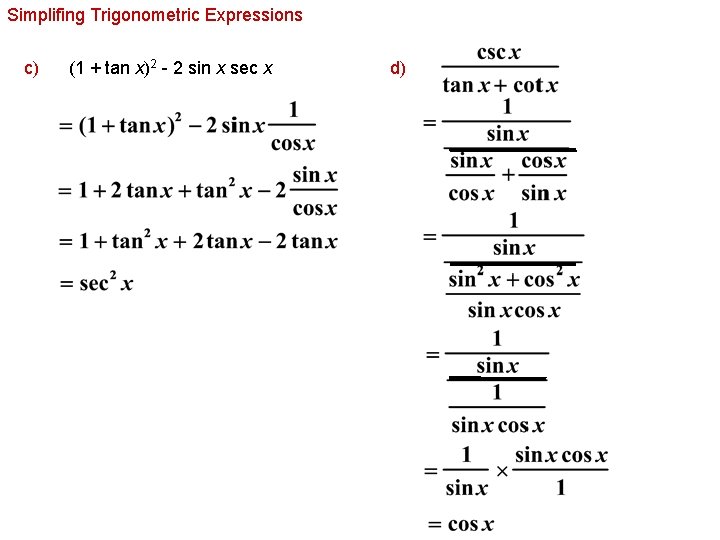



While You Wait Trigonometric Identities And Equations Section




Tangent Half Angle Formula Wikipedia
Trigonometric Identities Pythagoras's theorem sin2 cos2 = 1 (1) 1 cot2 = cosec2 (2) tan2 1 = sec2 (3) Note that (2) = (1)=sin 2 and (3) = (1)=cos Compoundangle formulae cos(A B) = cosAcosB sinAsinB (4) cos(A B) = cosAcosB sinAsinB (5) sin(A B) = sinAcosB cosAsinB (6) sin(A B) = sinAcosB cosAsinB (7) tan(A B) = tanA tanB 1 tanAtanB (8) tan(A B) = tanA tanB 1There are some trigonometric identities which you must remember in order to simplify trigonometric expressions when required These are \{\sin ^2}x {\cos ^2}x = 1\Trig HalfAngle Identities The halfangle identities are the identities involving functions with half angles The square root of the first two functions sine and cosine take negative or positive value depending upon the quadrant in which θ /2 lies Here is a table depicting the halfangle identities
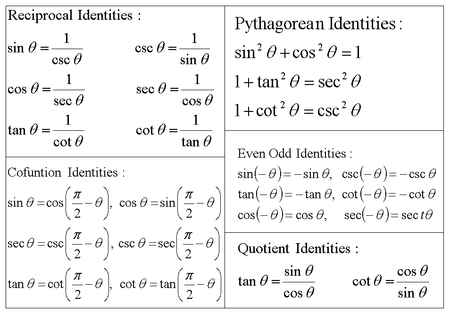



What Does It Mean To Prove A Trigonometric Identity Socratic



1
You would need an expression to work with For example Given #sinalpha=3/5# and #cosalpha=4/5#, you could find #sin2 alpha# by using the double angle identityTrig identities tan^2Section 71 Solving Trigonometric Equations and Identities 413 Try it Now 2 Solve 2 2sin ( ) 3cos(t t ) for all solutions t 0 2 In addition to the Pythagorean identity, it is often necessary to rewrite the tangent, secant,Periodicity of trig functions Sine, cosine, secant, and cosecant have period 2 π while tangent and cotangent have period π Identities for negativeNow, using the trigonometric identity 1tan 2 a = sec 2 a sec 2 A = 1 (3/4) 2 sec 2 A = 25/16 sec A = ±5/4 Since, the ratio of lengths is positive, we can neglect sec A = 5/4 Therefore, sec A = 5/4 Example 2 (1 – sin A)/(1 sin A) = (sec A – tan A) 2 Solution Let us take the Left hand side of the equation LHS = (1 – sin A)/(1 sin A) Multiply both numerator and




Trigonometric Identities




14 2 Trigonometric Identities
Tan(x y) = (tan x tan y) / (1 tan x tan y) sin(2x) = 2 sin x cos x cos(2x) = cos ^2 (x) sin ^2 (x) = 2 cos ^2 (x) 1 = 1 2 sin ^2 (x) tan(2x) = 2 tan(x) / (1To integrate tan^22x, also written as ∫tan 2 2x dx, tan squared 2x, (tan2x)^2, and tan^2(2x), we start by utilising standard trig identities to change the form of the integral Our goal is to have sec 2 2x in the new form because there is a standard integration solution for that in formula booklets that we can use We recall the Pythagorean trig identity, and multiply the angles by 2 Section 12 Integrals Involving Trig Functions In this section we are going to look at quite a few integrals involving trig functions and some of the techniques we can use to




Ppt Analytic Trig Powerpoint Presentation Free Download Id




Fundamental Identities
In this video I go over the proof of the trigonometry identity tan^2(x) 1 = sec^2(x) The proof of this identity is very simple and like many other trig idThe key Pythagorean Trigonometric identity are sin 2 (t) cos 2 (t) = 1 tan 2 (t) 1 = sec 2 (t) 1 cot 2 (t) = csc 2 (t) So, from this recipe, we can infer the equations for different capacities additionally Learn more about Pythagoras Trig Identities Dividing through by c 2 gives a 2/ c 2 b 2/ c 2 = c 2/ c 2 This can be simplified to (a/c) 2 (b/c) 2 = 1 Now, a/c is OppositeThe key Pythagorean Trigonometric identity is sin 2 (t) cos 2 (t) = 1 tan 2 (t) 1 = sec 2 (t) 1 cot 2 (t) = csc 2 (t) So, from this recipe, we can infer the equations for different capacities additionally Recall of Pythagoras Theorem You are going to need to rapidly review the three Pythagorean Identities The first Trig Identity of Pythagoras Theorem is very simple and easy to




Trigonometric Identities Sin 2 X Cos 2 X Tan 2 X Youtube




Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube
List of trigonometric identities 2 Trigonometric functions The primary trigonometric functions are the sine and cosine of an angle These are sometimes abbreviated sin θ) and cos(θ), respectively, where θ is the angle, but the parentheses around the angle are often omitted, eg, sin θ and cos θ The tangent (tan) of an angle is the ratio of the sine to the cosine Finally, theExample 6 Verify the identity tan (α/2) = (1 − cos α)/sin α Example 7 Verify the identity tan (α − 2) = sin π/(1 cos α) Begin with the identity in Example 6 Example 8 Use a half‐angle identity for the tangent to find the exact value for tan 15° What follows are two alternative solutions Previous Double Angle and Half Angle Identities Next Product Sum and Sum ProductThe other four trigonometric functions (tan, cot, sec, csc) can be defined as quotients and reciprocals of sin and cos, except where zero occurs in the denominator It can be proved, for real arguments, that these definitions coincide with elementary geometric definitions if the argument is regarded as an angle given in radians Moreover, these definitions result in simple expressions
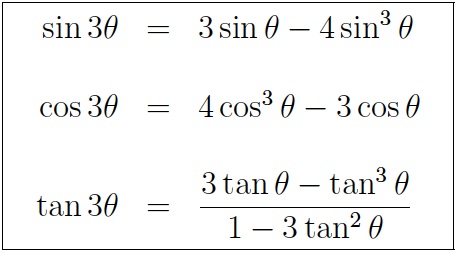



Summary Of Trigonometric Identities




Trigonometric Identities List Of Trigonometric Identities Examples
Tan adjacent q= adjacent cot opposite q= Unit circle definition For this definition q is any angle sin 1 y q==y 1 csc y q= cos 1 x q==x 1 sec x q= tan y x q= cot x y q= Facts and Properties Domain The domain is all the values of q that can be plugged into the function sinq, q can be any angle cosq, q can be any angle tanq, 1,0,1,2, 2 qpnnTangent and cotangent identities Pythagorean identities Sum and difference formulas Doubleangle formulas Halfangle formulas Products as sums Sums as products A N IDENTITY IS AN EQUALITY that is true for any value of the variable (An equation is an equality that is true only for certain values of the variable) In algebra, for example, we have this identity (x 5)(x − 5) = x 2Sin 2Acos A =1 wecandividethroughbycos2 A togive sin2 A cos2 A cos2 A cos 2A = 1 cos A But sinA cosA =tanA and 1 cosA =secA (Notethat thedefinitionofthesecantofA is 1 cosA) Hence tan2 A1=sec2 A Thisisanotherimportantidentity Key Point tan2 A1=sec2 A Onceagain,returningto sin 2Acos A =1 wecandividethroughbysin2 A togive sin2 A sin 2A
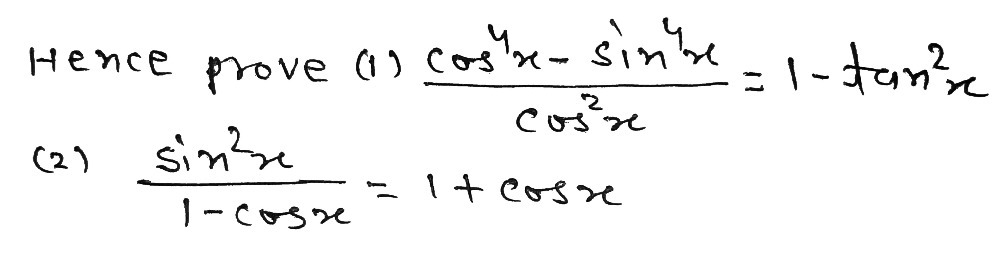



L Smsocosr Z1 In The Interval B Prove The Followi Gauthmath



How I Remember Trig Identities Part 2 Beyond Solutions
Using Trig Identities to Solve a Quadratic in Sin x Category Mathematics In the first of this pair of Casio videos, the identity sin 2 x cos 2 x≡ 1 is used to solve fully the equation 9sin 2 x 21sinx = 3cos 2 x 12 The second video explores how a graphical calculator can be used to find solutions of the equation by plotting both sides of the equation we are trying to solve, andTrig identities tan^2 Trig identities tan^2Trigonometric Identities Pythagoras's theorem sin2 cos2 = 1 (1) 1 cot2 = cosec2 (2) tan2 1 = sec2 (3) Note that (2) = (1)=sin 2 and (3) = (1)=cos CompoundThe half‐angle identity for tangent can be written in three different forms In the first form, the sign is determined by the quadrant in which the angle α/2 is located Example 5 VerifySome Useful Trigonometric Identities An identity is an equation whose left and right sides when defined are always equal regardless of the values of the variables the two sides contain Some very useful trigonometric identities are shown below The Pythagorean Identities $$\begin{array}{c} \cos^2 \theta \sin^2 \theta = 1\\ 1 \tan^2 \theta = \sec^2 \theta\\ 1 \cot^2 \theta = \csc^2




Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube




Trigonometric Identities And Examples With Worksheets
Trigonometric identities 18 Ma 2 MathRef Various identities and properties essential in trigonometry Legend x and y are independent variables, d is the differential operator, int is the integration operator, C is the constant of integration Identities tan x = sin x/cos x equation 1 cot x = cos x/sin x equation 2 sec x = 1/cos x equation 3 csc x = 1/sin x equation 4 cot x = 1/tan Here we will prove the problems on trigonometric identities As you know that the identity consists of two sides in equation, named Left Hand Side (abbreviated as LHS) and Right Hand Side (abbreviated as RHS)To prove the identity, sometimes we need to apply more fundamental identities, eg $\sin^2 x \cos^2 x = 1$ and use logical steps in order to lead one



Trigonometric Identities



Complex And Trigonometric Identities Introduction To Digital Filters




Trig Identities Maple Learn Maplesoft



Proving Trig Identities C3 Help The Student Room




Tangent Half Angle Formula Wikipedia




Trigonometric Identities Topics In Trigonometry




Exam Questions Trigonometric Identities Examsolutions




Example 1 Verify A Trigonometric Identity The Left Hand Side Of This Identity Is More Complicated So Transform That Expression Into The One On The Right Ppt Download




11 Tips To Conquer Trigonometry Proving
x-1=sec(squared)x.jpg)



10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com




Lesson 5 2 Verifying Trigonometric Identities By Griffin Heier




Lesson 22 Trigonometric Identities Ib Math Hl




Basic Trigonometric Identities And Equations Ppt Download




Integrate Sec 2x Method 1
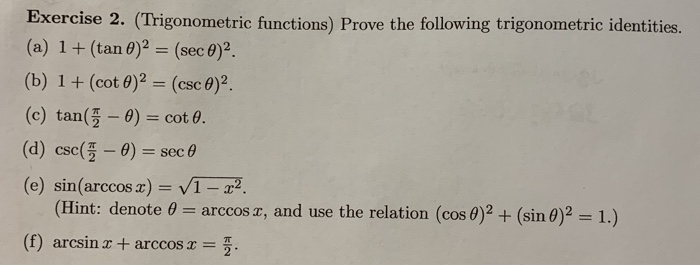



Solved Exercise 2 Trigonometric Functions Prove The Chegg Com




Summary Of Trigonometric Identities
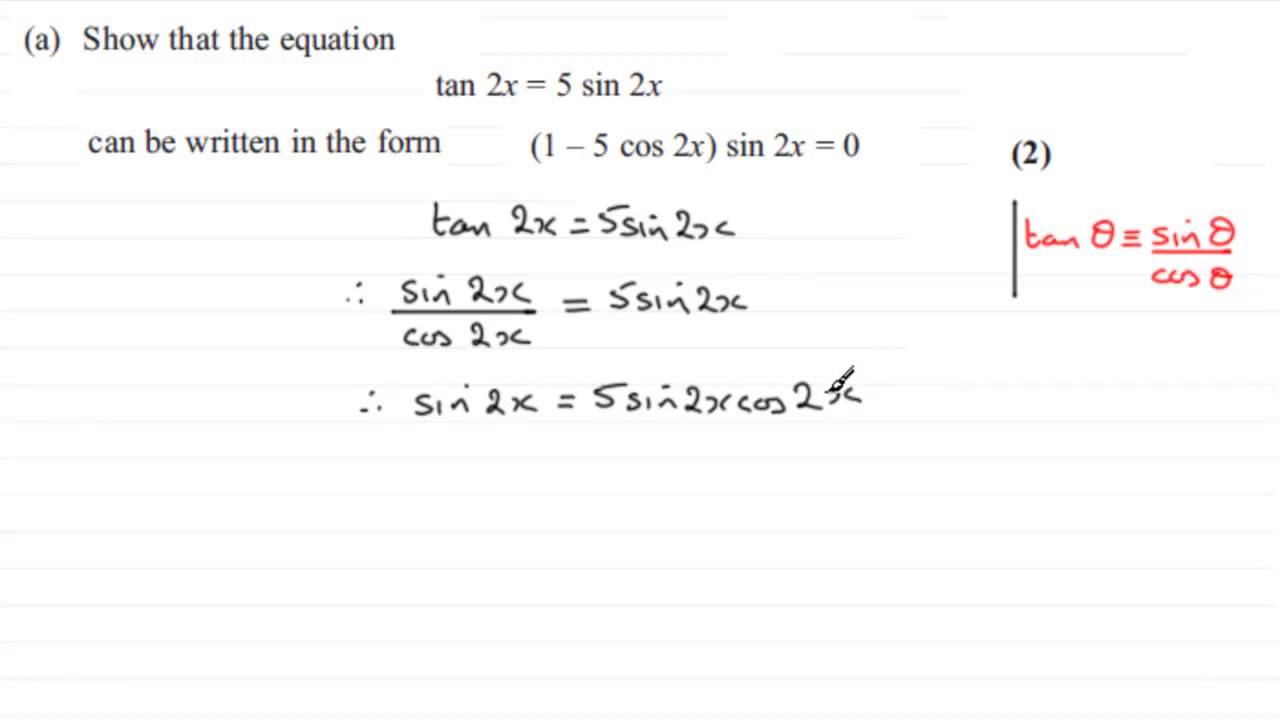



Exam Questions Trigonometric Identities Examsolutions




Solved Inquiry 11 8 Marks Prove The Following Trig Identities Tan 2x 2tan 2xsin X Sin2x Marks B Sec X 2secxcosx Cos X Tan X Sin 5 Marks 12 12 2 Marks Determine The Exact Value




Trig Identities Bingo Card




Trig Identities Study Sheet



Ilectureonline
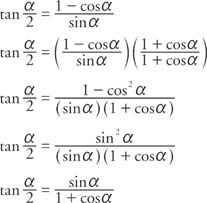



Tangent Identities
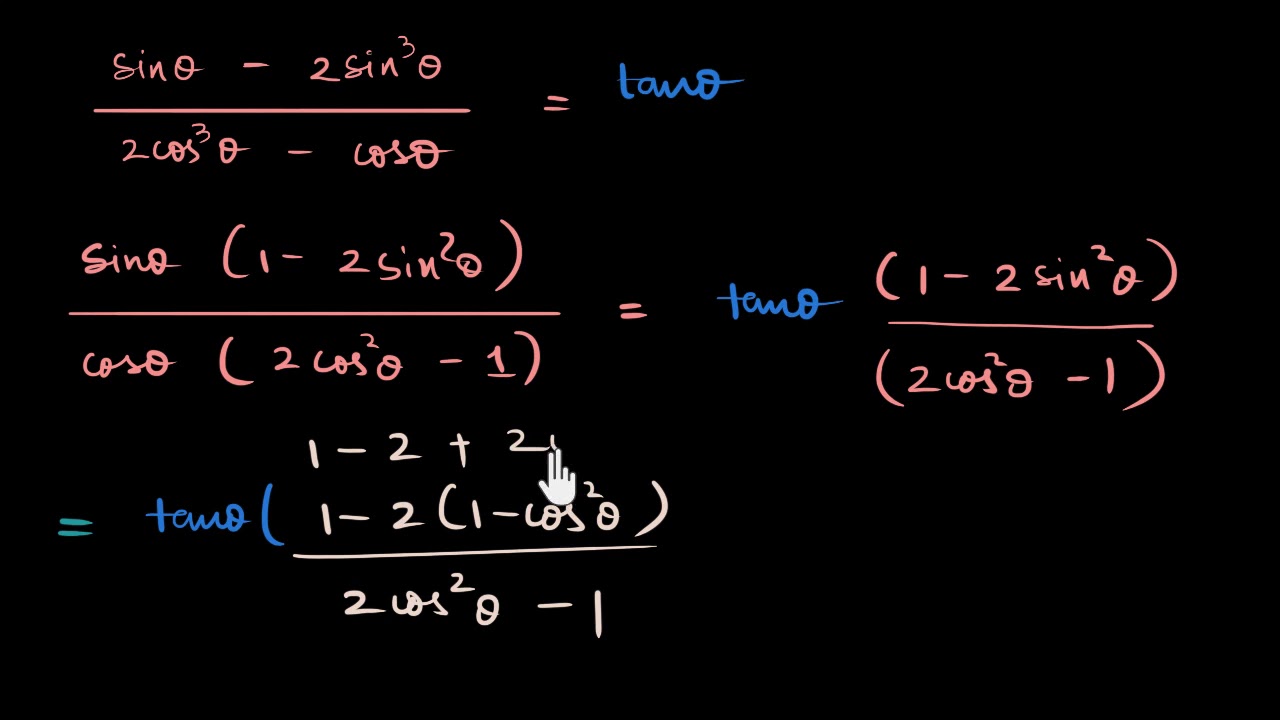



Trigonometric Identity Example Proof Involving Sin Cos And Tan Video Khan Academy




How Do You Verify The Identity Tan2theta 2 Cottheta Tantheta Socratic




How To Solve Tan 2xsin 2x Tan 2x Sin 2x Trigonometry Trigonometric Identities Youtube



Verifying Trigonometric Identities How To Do It The Easy Way Lesson Plan Spiral




How Do You Use The Fundamental Trigonometric Identities To Determine The Simplified Form Of The Expression Socratic




5 1 Fundamental Trig Identities Reciprocal Identities Sin




Cos 2x Formula Derivation Examples What Is Cos 2a Formula
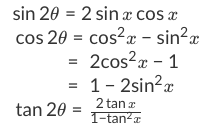



How To Use Double Angle Identities Studypug




Trigonometric Identities 1 Conditional Trigonometrical Identities We Have Certain Trigonometric I Simplifying Expressions Maths Formulas List Maths Solutions



A Trig Identity



2
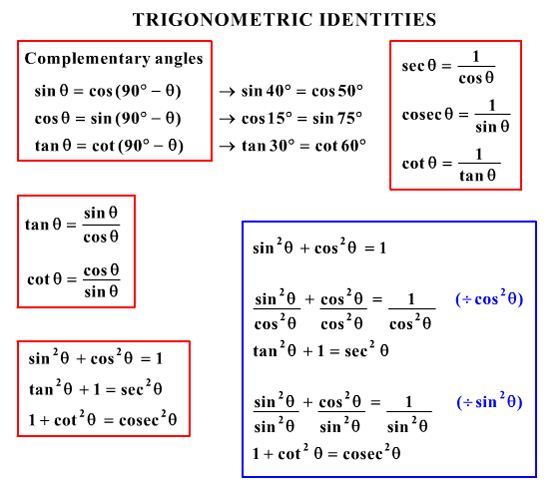



How To Solve Tan 2y Sec 2y Tan 4y Tan 2y Socratic




Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Lowering Power Tan 2 X Youtube



1




Trigonometric Identities Edexcel A Level Maths Pure Revision Notes




Trig Identities Bingo Card




List Of Trigonometric Identities Wikipedia




7 4 Proving Trigonometric Identities In This Unit We Ll Be Using Some Formula S That Are Also Found And Used In Unit 7 2 And 7 3 Here We Ll Be Solving Problems To Show That Both Sides Of The Equation Equal Each Other These Formulas Will Help Solve Some Trig




Solved Proving Trigonometric Identities Q1 Prove That Sin 2x Chegg Com




Tangent Identities
.JPG)



Every Day I M Calculatin I D3 Unit Q Pythagorean Identities
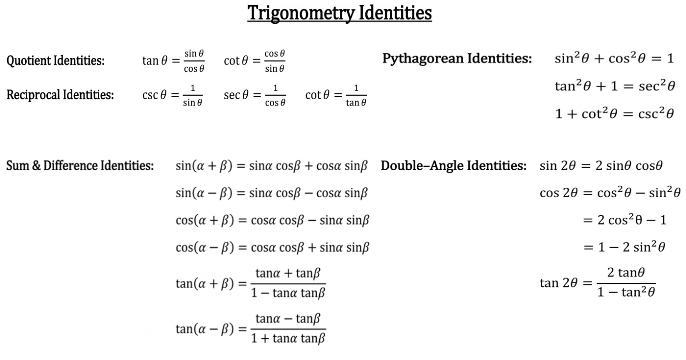



How To Prove Quotient And Reciprocal Identities Studypug




Understanding Pythagorean Identities Studypug



3



1




Cos Sin Tan Csc Sec Cot




Verifying A Trigonometric Identity Tan 2 X 1 Sec X Sec X Youtube



Complex And Trigonometric Identities Introduction To Digital Filters




Trigonometric Identities Proofs List Of Trig Identities




Integrate Tan 2x




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Worksheet On Finding The Unknown Angle Using Trigonometric Identities




Trig Identities Bingo Card




Trigonometric Identities Simplify Expressions Video Lessons Examples And Solutions




上 Tan2x Identity ただの悪魔の画像



What Is The Formula Of Tan2x Quora



Important Trigonometric Identiti



2




Trigonometric Identities




Solved 2 Prove The Following Trig Identities A Prove Tan Chegg Com
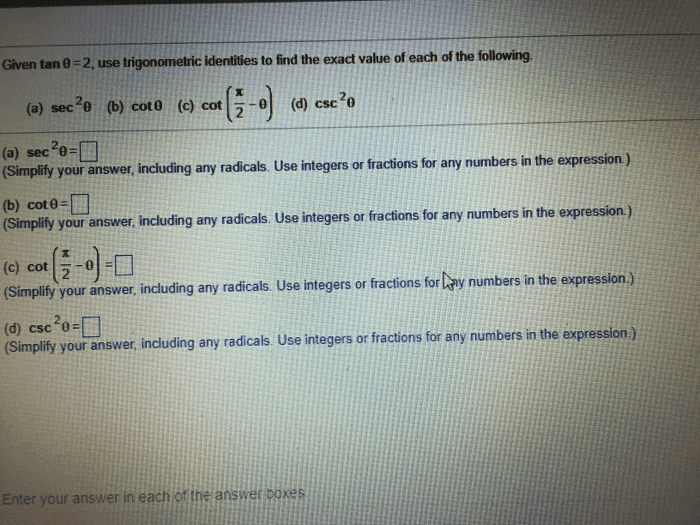



Oneclass Tan 0 2 Use Trigonometric Identities To Find The Exacd Value Of Each Of The Following A
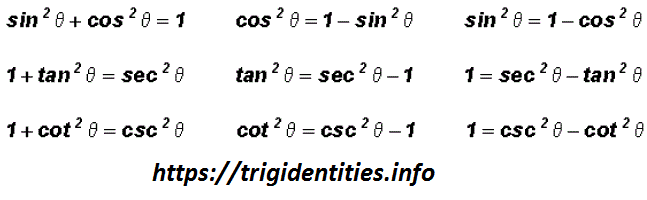



Pythagorean Trig Identities Recall Pythagoras Theorem Trig Identities




14 2 Trigonometric Identities




How To Use Trig Identities Mathematics Stack Exchange
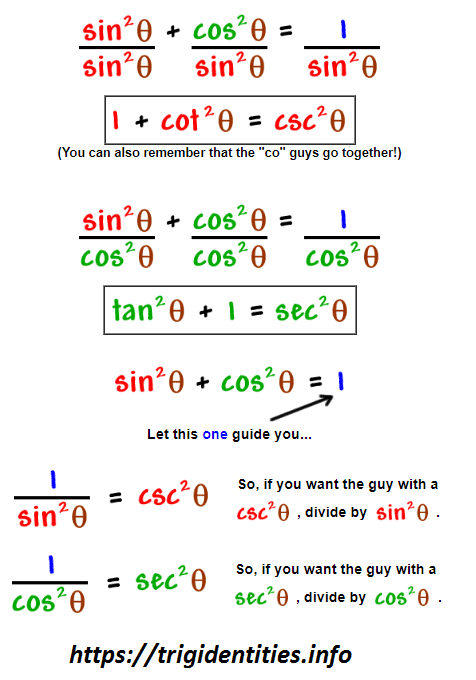



Pythagorean Trig Identities Recall Pythagoras Theorem Trig Identities




Trigonometric Identities Edexcel A Level Maths Pure Revision Notes




Worksheet On Trigonometric Identities Establishing Identities Hints



6 1 2 Trigonometric Identities




Summary Of Trigonometric Identities



Trigonometry Identities



Trig Identities Hsn Forum




Summary Of Trigonometric Identities




Summary Of Trigonometric Identities
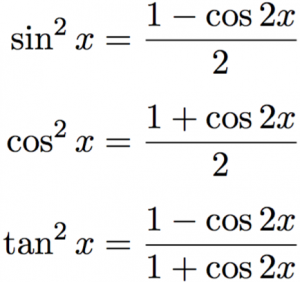



Trig Identities Table Of Trigonometric Identities



2
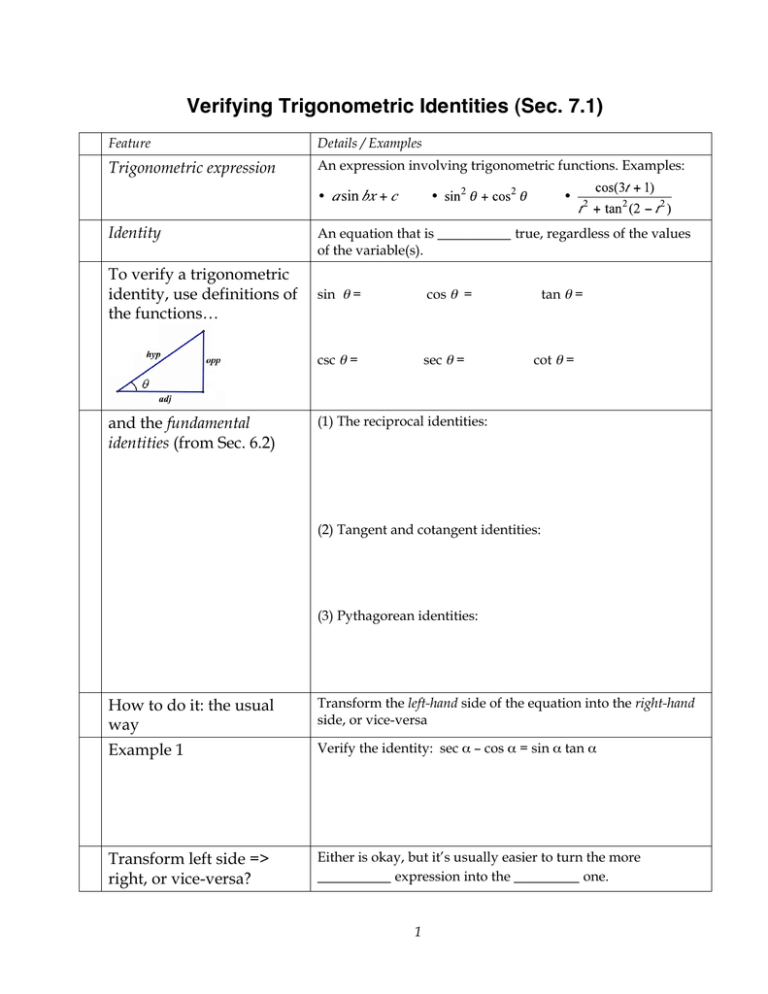



Verifying Trigonometric Identities Sec 7 1 Trigonometric Expression Identity




Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download



Trig Identities Hsn Forum
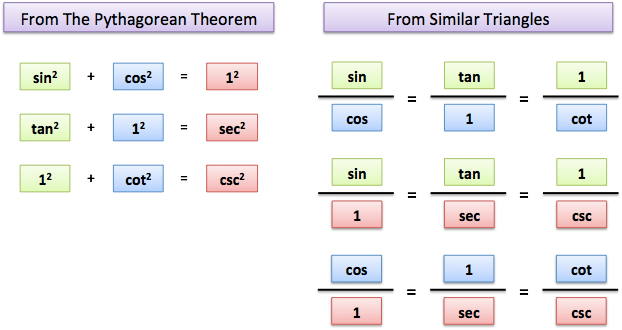



Easy Trig Identities With Euler S Formula Betterexplained
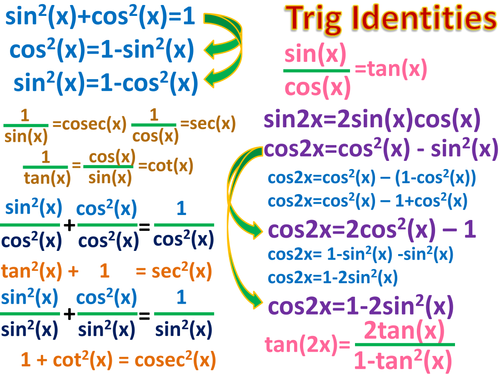



Trigonometry Identities Poster Teaching Resources




Solved Inquiry 11 8 Marks Prove The Following Trig Chegg Com
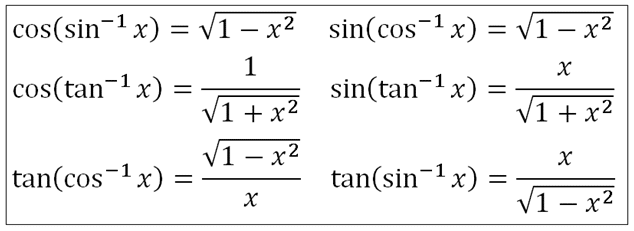



Inverse Trig Identities Reciprocal Of Trigonometric Function Trig



0 件のコメント:
コメントを投稿